When people think of voxels, they often associate them implicitly with cubes. This isn't really surprising; it is the most intuitive way to subdivide 3D space.

The humble cube.
There are many advantages to doing this, simplicity being one of them. It is fast to index, and easy to reason about.
If your virtual world is a flat, infinite plane (eg. Minecraft and all its clones), then cubes fit very well. The problems start to occur when the world is spherical.
It is impossible to map a sphere onto a flat plane without distortion. Cartographers have known this for centuries. The most popular map projection, Mercator, famously suffers from the problem of inflating the size of countries near the poles. The benefit is that straight lines on a Mercator projection correspond to a fixed bearing relative to North (rhumb lines), which made it extremely useful for navigation.
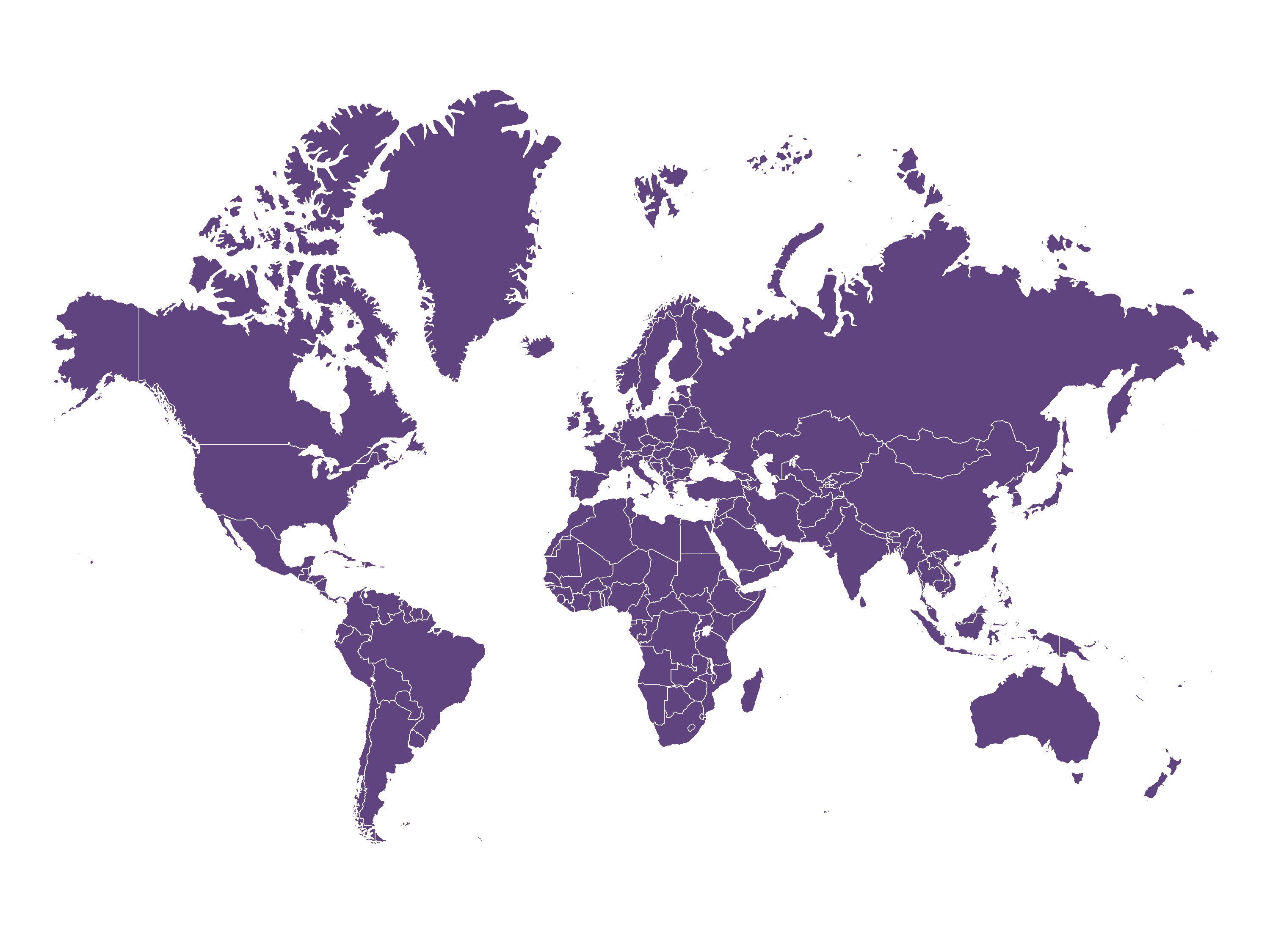
The Mercator projection, with Greenland appearing as large as Africa.
Why do we care? Just make the whole planet out of voxels. This technically works, but if you are using bloxels or marching cubes, then your grid will be misaligned with the planets gravity vector depending on where you are on the planet.
Another issue is efficiency. If your game loop doesn't include players burrowing into the center of a planet (eg. Astroneer) then a large portion of the planet is wasted space. I see a recurring theme among voxel engine developers to maximise the scale of their simulations. This is fun, and some players will leave comments about how amazing it is, but usually leads to very boring gameplay.
As an example, Minecraft only takes place in a comparatively thin slice of voxel data. For a long time, the world was only 127 blocks high. That has since been increased to 383, which is about the height of hills (not mountains) in real life.
A Thin Slice
An alternative is to only have voxels on the surface of the planet. All of the gameplay can occur on this appleskin. This may seem limiting, but interesting things generally happen on phase transitions, not steady-state.
At this point, we have to address the topological elephant in the room. How to map our voxel chunks to a sphere?
The most obvious way is to use the faces of a cube. Subdivide it enough, and you have the resolution for detailed planetary surfaces. Normalise the points on the cube to form a sphere, and you have the initial topology for a voxel planet:
This has its own set of problems. The most prominent: what is happening on the corners?
For one, the squares are no longer square. They've become squishy rhombi. Secondly, they cluster around the corners, much more huddled together than the center of the cube faces.
The latter problem is solvable. Simply push the vertices away from the corners so they are better distributed. This is accomplished with the following equation, which maps points on the cube to the new points on a sphere:
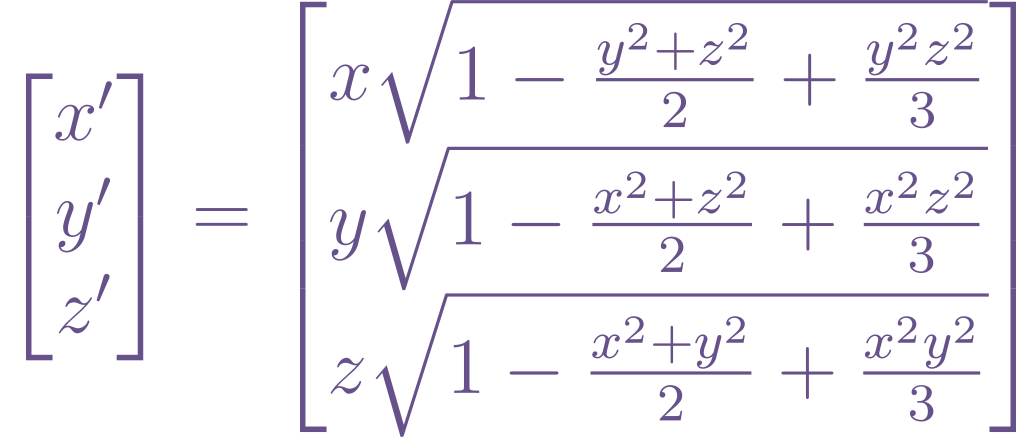
The derivation for this can be found here
You can see the effect this has when compared to the naive normalisation. The squares become less squished, and the sizes are more consistent:
This is an improvement, but a fundamental aspect of this mapping is the 120 degree angle at the corners. We will always be trying to connect those 3 cube faces together, resulting in square chunks that have to distort to odd shapes.
Other Solids
What if we ditched squares? They're not the only shape we can use to tile a surface.
There are other platonic solids we could have started with. Let's see what happens if we subdivide other solids:
One of these stands out as exceptionally isotropic. The icosahedron, when subdivided, minimises distortion much better compared to the other solids.
This is great; we can even tweak it into slightly different shapes that have their own useful properties:

It is a little disappointing that there are still 5 triangles at the original corners, while most of the surface has 6. This is an invariant of geometry that cannot be violated for subdivided surfaces.
Simplicity of Simplexes
So if we want to use subdivided icosahedrons as the base for a voxel planet, cubic voxels aren't gonna cut it. We will have to use a shape with a triangular base.
Tetrahedrons may come to mind, but it is more annoying to tile space with them.
Triangular prisms are more suitable for this, as they can be subdivided into an octree structure easily:
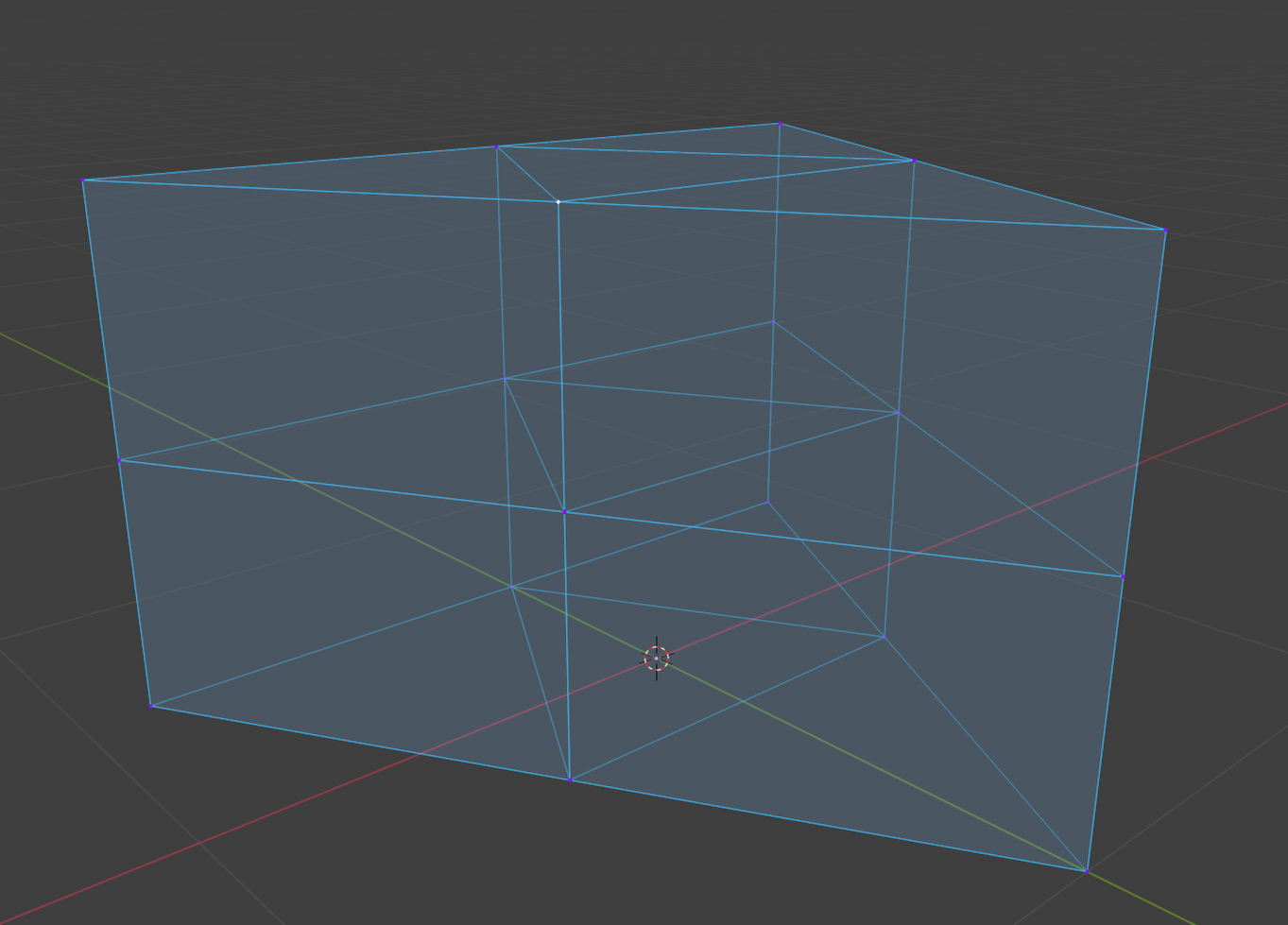
Indexing triangular prism chunks is not as easy as cubes, since the stride changes.
Comments
Set a username to leave comments:
Commenting as: